Topic 2

Jump to: Motion 2.1 Forces 2.2 Work, energy, and power 2.3 Momentum 2.4 Topic 2 Problems

2.1 Motion

Displacement and Distance

Velocity and Speed

Velocity	Speed
-Vector Rate of change of displacement in respect to time	-Scalar Rate of change of distance in respect to time

Velocity is a measure dependent on the motion of the observer. The relative velocity of A to B is equal to the vector subtraction of the velocity of B from the velocity of A.

Acceleration

Acceleration
-Vector Rate of change of velocity in respect to time

*Acceleration due to gravity = 9.8 m/s². Does not depend on mass of the object.
**Acceleration is a vector and thus has a direction. If we assume the upwards direction to be positive, the acceleration due to gravity would have a negative value.

Motion Graphs

Displacement-time graph

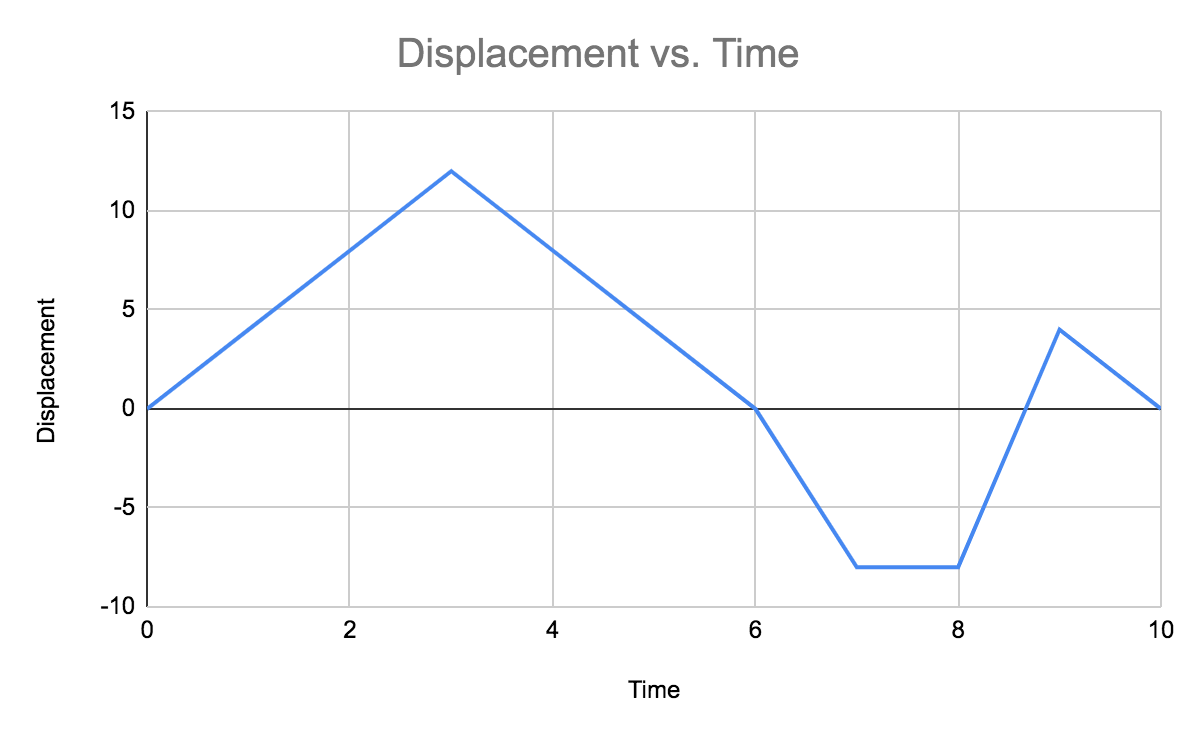
*Slope is velocity

Velocity-time graph

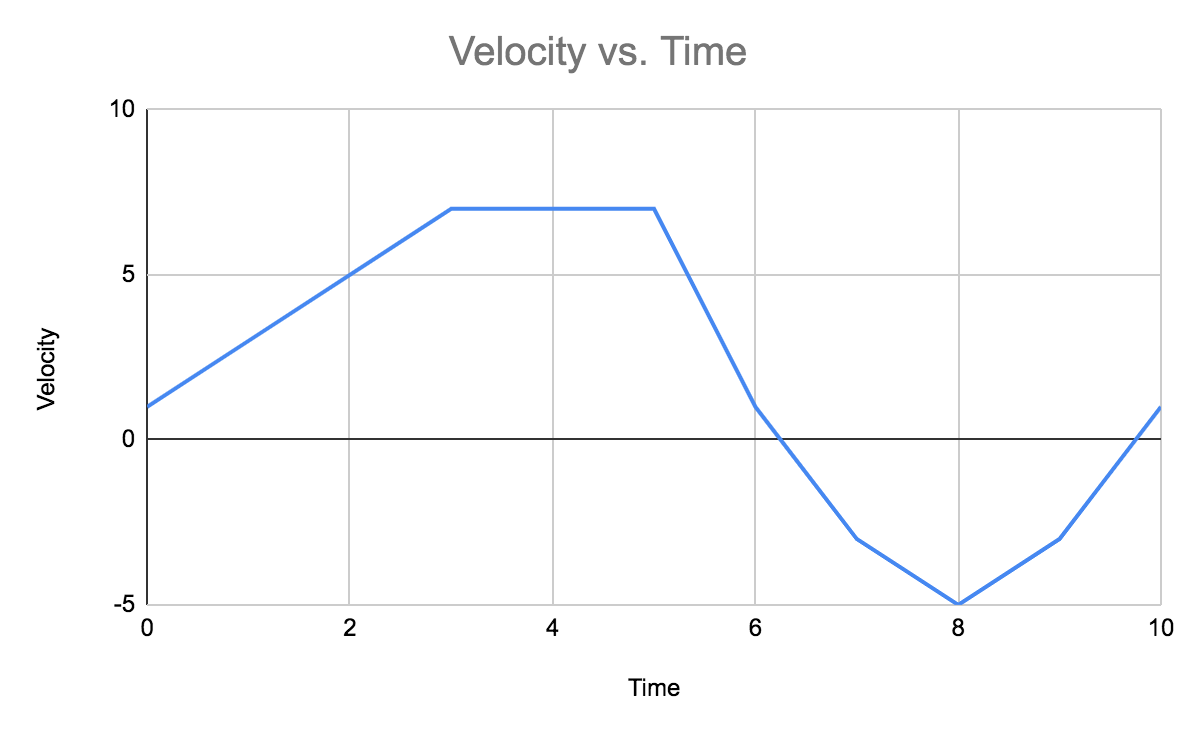
*Slope is acceleration **Area under the curve is displacement

Acceleration-time graph

*Area under the curve is change in velocity

Understanding with calculus

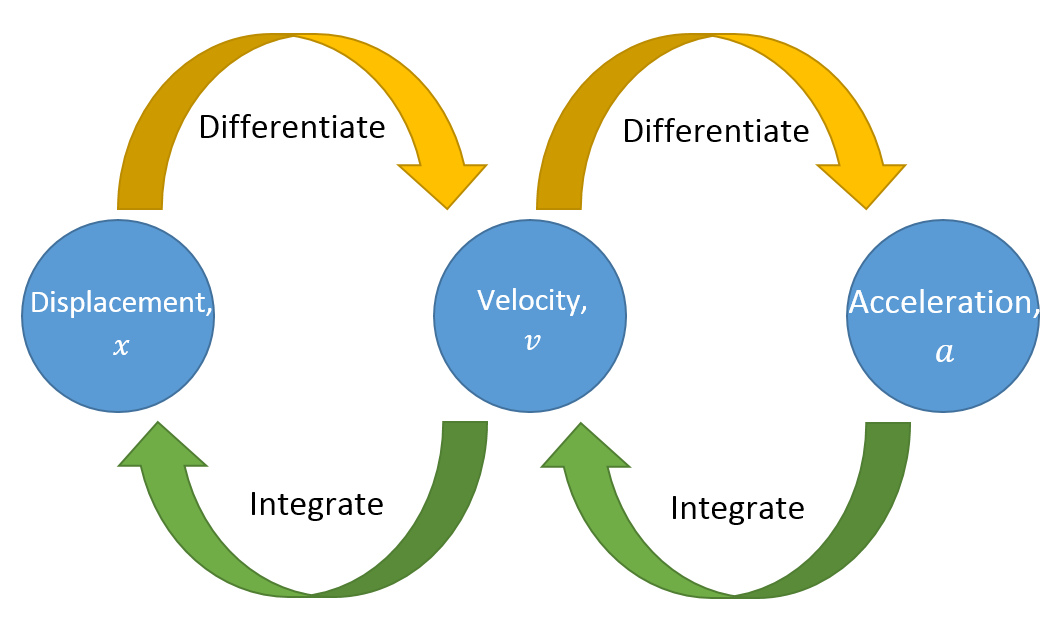Motion graphs help tool

Suvat equations

*acceleration must be constant!

\begin{matrix} v = u + a t \\ s = \frac{(u + v)}{2} t \\ s = u t + \frac{1}{2} a t^{2} \\ s = v t - \frac{1}{2} a t^{2} \\ v^{2} = u^{2} + 2 a s \\ v = f i n a l v e l o c i t y, u = i n i t i a l v e l o c i t y, t = t i m e t a k e n, s = d i s p l a c e m e n t, a = a c c e l e r a t i o n \end{matrix}

Projectile motion

An object follows a curved path due to the influence of gravity.

If no air resistance:

The horizontal component is constant

The vertical component accelerates downward at 9.81 ms^-2

The projective reaches maximum height when vertical velocity is 0

The trajectory is symmetric

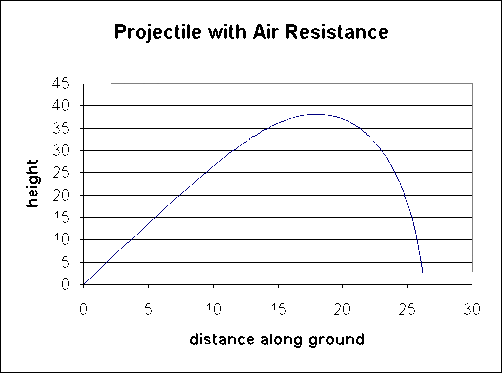
If air resistance is present:

The maximum height is lower

The trajectory is not symmetric

The range of projectile is shorter

Terminal velocity

When the force of air resistance is equal to the force of gravity on a falling object

The specific velocity at which one stops accelerating is known as terminal velocity

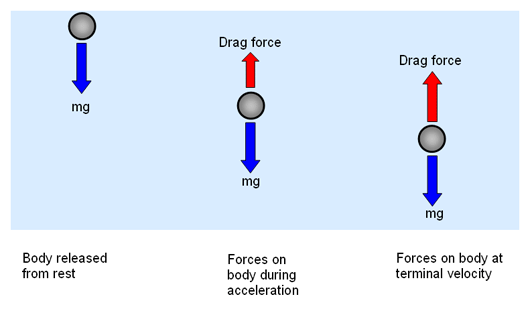
\begin{matrix} v = \sqrt{\frac{2 m g}{ρ A C_{d}}} \\ m = m a s s, g = a c c e l e r a t i o n d u e t o g r a v i t y, ρ = d e n s i t y o f m e d i u m, A = a r e a o f o b j e c t, \\ C_{d} = d r a g c o e f f i c i e n t o f o b j e c t \end{matrix}

Table of common drag coefficients

2.2 Forces

Free body diagrams

ForcesUnit of force is Newtons are represented as arrows acting on a point mass.

The lenght and direction depends on the magnitude and direction of the force.

To determine resultant force:

1.Resolve the forces into vertical and horizontal components

2.Combine the sum of horizontal and vertical components

3.Find the angle by using tangent

Transitional equilibrium

The net force on the body is zero, so the body is at rest or travels at constant velocity.

Examples: elevator moving upwards at constant velocity, a falling man reaches terminal velocity.

Newton's laws of motion

Published in Philosophiae Naturalis Principia Mathematica (1687)

1.If a body is at rest or moving at a constant speed in a straight line, it will remain at rest or keep moving in a straight line at constant speed unless it is acted upon by a force. This postulate is known as the law of inertia.

2.F=ma

3.When two bodies interact, they apply forces to one another that are equal in magnitude and opposite in direction. The third law is also known as the law of action and reaction.

Friction

FrictionDenoted by µ is a force opposing motion, where to solid surfaces move against each other.

There are two types of friction for solids: static (stops object from beggining motion) and kinetic (slows down objects motion).

Static friction (µs) is larger than kinetic friction(µk).

\begin{matrix} F = µ N \\ F = f r i c t i o n a l f o r c e, µ = f r i c t i o n a l c o e f f i c i e n t, N = n o r m a l f o r c e \end{matrix}

Table of common frictional coefficients

2.3 Work, energy, and power

Kinetic energy

\begin{matrix} E_{k} = \frac{1}{2} m v^{2} \\ m = m a s s, v = v e l o c i t y \end{matrix}

Gravitational potential energy

\begin{matrix} E_{p} = m g h \\ m = m a s s, g = a c c e l e r a t i o n d u e t o g r a v i t y, h = h e i g h t \end{matrix}

Elastic potential energy

\begin{matrix} E_{p} = \frac{1}{2} k x^{2} \\ k = s p r i n g c o n s t a n t, x = e x t e n s i o n o f s p r i n g \end{matrix}

Work done

\begin{matrix} W = F * s * c o s θ \\ F = f o r c e, s = d i s p l a c e m e n t, θ = a n g l e b e t w e e n f o r c e a n d d i r e c t i o n o f m o t i o n \end{matrix}

In a force-displacement graph, work is the area under the curve

Power

\begin{matrix} P = \frac{W}{t} \\ W = w o r k d o n e, t = t i m e t a k e n \end{matrix}

For a constant force acting on object with constant velocity:

\begin{matrix} P = v F \\ F = f o r c e, v = v e l o c i t y \end{matrix}

Conservation of energy

Energy cannot be created or destroyed, only converted into different form. For example when kicking a football that is sitting on the ground, energy is transferred from the kicker's body to the ball, setting it in motion.

Demonstration of the conservation of energy

Total energy remains constant:

\begin{matrix} Δ K E + Δ P E = 0 \end{matrix}

Efficiency

E f f i c i e n c y = \frac{u s e f u l e n e r g y o u t p u t}{e n e r g y i n p u t} * 100 %

E f f i c i e n c y = \frac{u s e f u l p o w e r o u t p u t}{p o w e r i n p u t} * 100 %

2.4 Momentum

Linear momentum

\begin{matrix} L i n e a r m o m e n t u m i s g i v e n b y : \\ p = m v \\ v = v e l o c i t y, m = m a s s, p = m o m e n t u m \end{matrix}

It is a vector with the same direction as the velocity
The change of momentum is called impulse

Impulse formula

\begin{matrix} F Δ t = m Δ v \\ F Δ t i s t h e i m p u l s e, m = m a s s, v = v e l o c i t y \end{matrix}

Impulse and force-time graphs

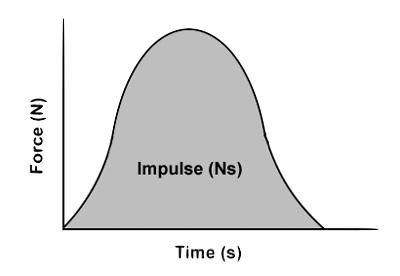
The area under the force-time graph is impulse

Conservation of linear momentum

In a closed system, the sum of initial momentum is equal to the sum of final momentum

\begin{matrix} m_{1} u_{1} + m_{2} u_{2} = m_{1} v_{1} + m_{2} v_{2} \\ m = m a s s, u = i n i t i a l v e l o c i t y, v = f i n a l v e l o c i t y \end{matrix}

Collisions

Type	Total Momentum	Total Kinetic energy
Elastic	Conserved	Conserved
Inelastic	Conserved	Not conserved
Explosion	Conserved	Not conserved